SPC控制图的管控界限UCL和LCL是基于3个标准差而得到的，而实际计算时，则是需要用A2，D3，D4来计算的，即A2，D3，D4是用来计算标准差，从而得到管控的上下限的。题主在实际运用中有这样的疑问，我估计是将样本的标准差和总体的标准差混淆了。可能您直接将收集的25组，每组5个数据，一共125个数据的标准差用来计算管控界限了，但这只是样本的标准差，而不是总体的标准差。那总体的标准差该如何估计呢（注意，只能是估计）？

假定质量特性服从正态分布,且,均已知。则样本均值,服从正态分布,并且样本均值落入界限:的概率为1-a。通常取,即采用3个标准差的做法。当然如果是非正态分布，根据中心极限定理，也可以得到这一推论。在实际工作中,μ与σ通常未知,这时就必须应用从稳态过程所取的预备样本的数据对它们进行估计。预备样本通常至少取25个(最好取35个预备样本)，样本大小n要取决于合理分组的结构,抽样与检查的费用,参数估计的效率等因素,n通常取为4、5、6。

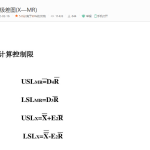
1.则过程的μ的最佳估计量为总均值,即可以采用作为图的中心控制线CL。

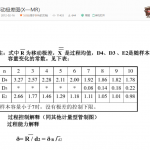
2.图建立控制界限UCL和LCL,需要估计过程的标准差σ，可以根据样本的极差或标准差来进行估计。应用极差进行估计的优点是极差计算简单。样本的极差,如果令W=R/σ,可以证明，W的期望值E(W)=,这是一个与样本大小n有关的常数,于是σ的估计量为=E(R)/。则,这就是A2的来由，同理LCL也得出。

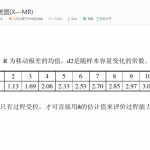
同样的方式在求R图的管制界限时，令W=R/σ,可以证明=(为一与样本大小n有关的常数),于是。

这样R图的控制上限，它的控制下限。这就是D3，D4的由来。